How many times have you sat in a meeting and heard the speaker say something to the effect of: “The difference between these two treatments was 15 hundredweight per acre, but that difference was not significant.” I say things like this in just about every presentation I give. Many times, I am approached afterward with this: “How can 15 hundredweight per acre not be significant? It’s significant to me.”
It is easy to understand why a person would feel that way. An additional 15 hundredweight (cwt) per acre means more money in your pocket, and that is significant to a crop producer. The problem is: The word “significant” means something different to the producer and the researcher. To the researcher, significant means “statistically different.” Understanding what this really means is economically important.
Now, please don’t flip to the next article just yet. The purpose of this column is not to drop into the deep waters of the statistics swimming pool. First of all, there is not enough space in this column to do the topic justice. Second, very few readers would want to swim in that pool to begin with. But it is important to explain why statistics are used in presenting research results and what the use of the word significant means.
Statistics can be descriptive or inferential – and even if we do not know it, we are familiar with both. Descriptive statistics simply summarize pieces of information in a meaningful way. Examples of descriptive statistics include the average spring wheat yield in 2021, the average rainfall in March or the average height of your local high school basketball team. These values convey useful information, but they do not allow us to make predictions. To make predictions, we need to use inferential statistics. Inferential statistics enable a researcher to make assumptions about a wider group using the characteristics of a representative, smaller group as a guide.
A good way to illustrate this is to talk about a fictional product I would like to sell you – I call it Miller’s Marvelous Masterpiece, or MMM for short. (I wanted to call it 3M, but I heard that name was already taken.) I hired an independent researcher to do a test with MMM. In that research trial, MMM had an average potato yield of 525 cwt per acre (Table 1).
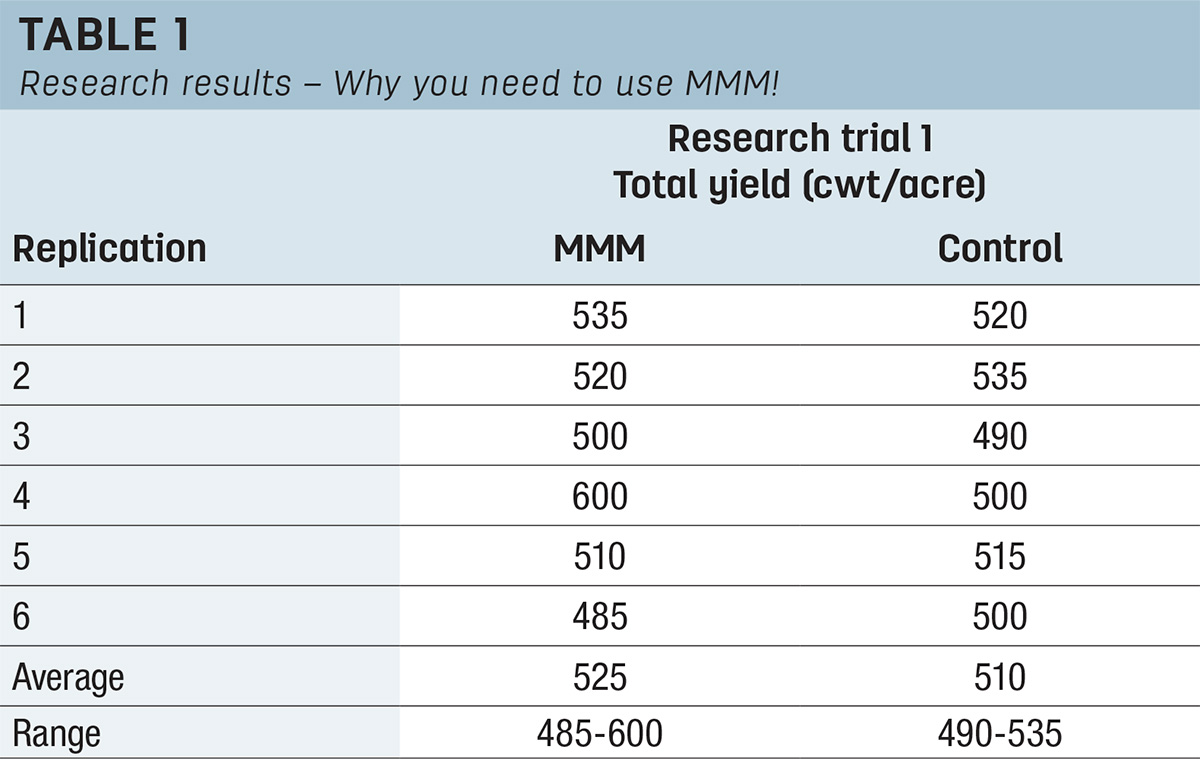
Potatoes not treated with MMM only yielded 510 cwt per acre. From this, it appears MMM increased potato yield by 15 cwt per acre – and at $8-per-cwt prices, this translates to an increased gross income of $120 per acre. Because I am such a nice person, I only charge $40 per acre for the product, leaving the producer a net gain of $80 per acre – a two times dollar return on investment.
But what if the researcher uses that phrase: “the differences were not significant.” Why does that matter when I have already shown you the average gross dollar increase was $120 per acre? This is where we get to the importance of understanding how the word “significant” is used. With any research trial, the term significant is attached to a degree of certainty. For example, we can be 90%, 95% or 99% certain the results were due to the treatment and not some other random factor.
Inferential statistics are used to understand more about those average yields reported by the researcher. Usually, research trials are done using replications, meaning each thing that is being tested is repeated multiple times. Many field trials will use four to six replications. In this case, the researcher used six. So, the question now becomes: How much did the six measurements vary from the average?
The six measurements (replications) for MMM in Research Trial 1 were scattered all over the board (Table 1). One plot of MMM measured 600 cwt per acre, and another measured 485. Additionally, out of the six replications in Research Trial 1, the control (potatoes not treated with MMM) had a higher yield than the MMM treatment in half of the replications. As a result, I can’t say with any degree of confidence that the MMM was responsible for that 15-cwt-per-acre increase. Based on the inconsistency between the yields, it looks like that difference was due to random variability. Put another way, if you buy and use MMM, there is a good chance you are not really going to see that $80-per-acre return on your investment. You might get the 600-cwt result, but you also might get the 485-cwt result.
The story would be different if the results were like what is shown in Research Trial 2 (Table 2).
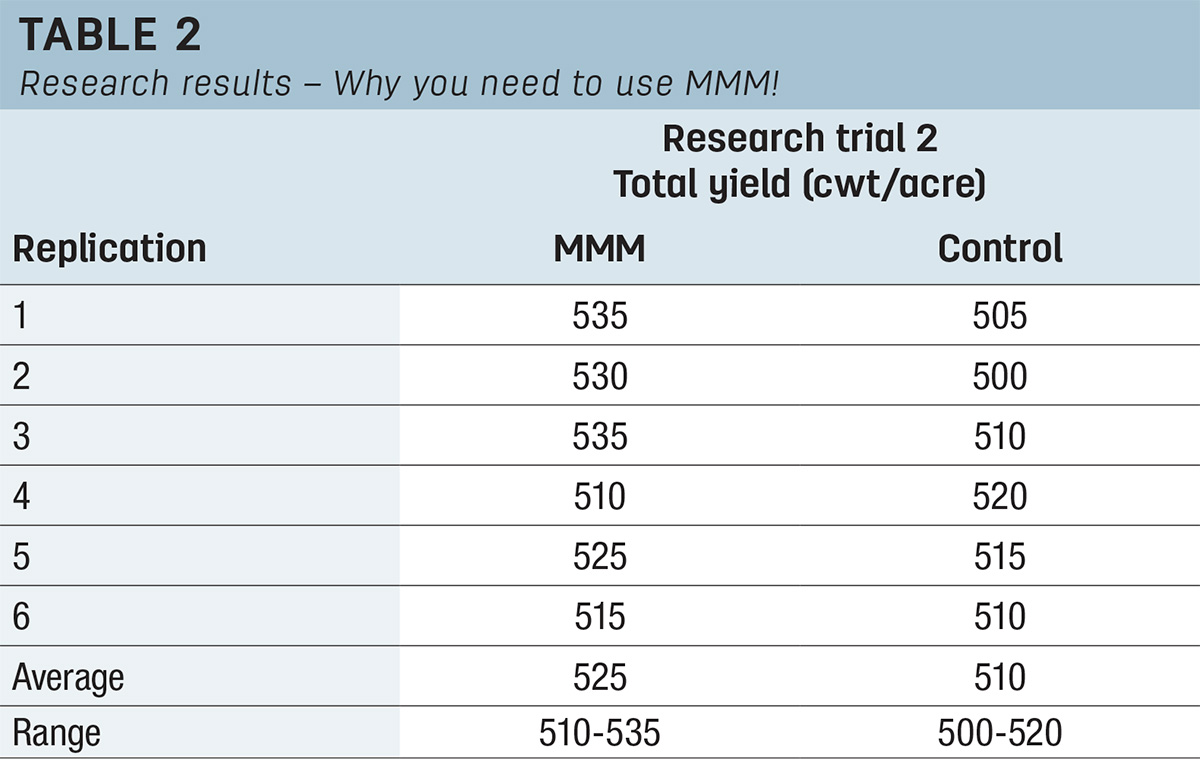
In this case, MMM was consistently higher than the control (five out of six replications). The likelihood is high that applying MMM will increase your yield. In other words, the difference in the yield in Research Trial 2 is “significant.”
And this is why we use statistics. It is a way to communicate the consistency behind measurements, allowing the audience to determine whether a research trial was more like Trial 1 or Trial 2.
The next question that usually comes after the meaning of significance is: Does small-plot research relate to what can happen in a real-world situation? Does it really translate?
Come back next time to find out. ![]()






